Forma desarollada

 

La expresión general o forma desarrollada o polinómica de una función cuadrática es la siguiente:

Deduciendo el vértice de la parábola a partir de los coeficientes de esta expresión...

Lo mejor es partir de la forma canónica (de la que ya sabemos bastantes cosas), desarrollarla y comparar lo que nos salga con esta expresión que acabamos de ver para sacar nuestras propias conclusiones.

Partimos entonces de la forma canónica:

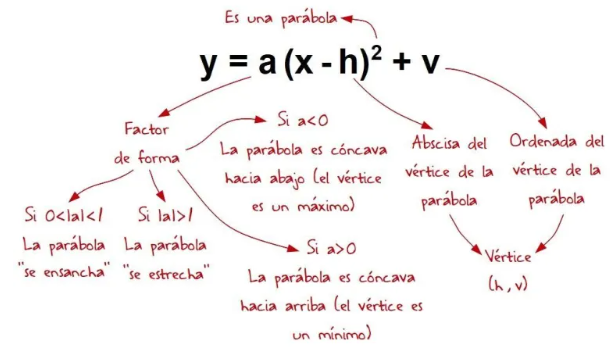
 y = a·(x-h)2 + v

desarrollando el binomio al cuadrado…

y = a·(x2+h2-2·x·h) + v

aplicando la propiedad distributiva del producto respecto de la suma…

y = ax2 + ah2 – 2ahx + v

y colocando términos, tenemos:

y = ax2 – 2ahx + ah2 + v

Si ahora comparamos esta expresión con la polinómica, tenemos que:

De donde deducimos que:

b = -2ah

c = ah2 + v

Pues a partir de ambas expresiones podemos obtener las coordenadas del vértice de la parábola en función de los coeficientes a, b y c.

Despejando h en la primera expresión obtenemos la abscisa del vértice de la parábola:

Despejando ahora v en la segunda expresión:

v = c – ah2

y sustituyendo después h por el valor anterior obtenido, conseguimos la ordenada del vértice de la parábola:

Es decir, el vértice de la parábola de la función cuadrática de ecuación desarrollada o polinómica  y=ax2+bx+c es:

Como has observado, esta forma desarrollada o polinómica no nos da directamente las coordenadas del vértice de la parábola, como sí lo hacía la forma canónica, aunque las podemos calcular a partir de los coeficientes a, b y c. Sin embargo sí nos da una información directa a través del coeficiente c que no nos daba la forma canónica: el punto de corte con el eje Y o eje de ordenadas, que sería el punto (0, c).

Esto que acabo de decir se deduce fácilmente ya que dicho punto es el que tiene como abscisa x=0, y si evaluamos la función en x=0 tenemos que:

y = 0·x2+0·x+c

y = c

Además seguimos teniendo la información que vimos que proporcionaba el coeficiente a en la forma canónica.

Resumiendo todo lo visto, a partir de la ecuación desarrollada o polinómica de una función cuadrática, podemos extraer la siguiente información: