Desplazamientos y retoques a la parábola

Retocando la representación gráfica de la función:

y = x2

Parábola vertical cuyo vértice está justo en el origen de coordenadas. Algo como esto…

Ahora, identificamos las partes:

Bien, ésta que acabamos de ver es la más sencilla de las funciones cuadráticas de una variable (nuestra variable es «x»), cuya expresión es un polinomio de segundo grado (el mayor exponente al que está elevada la variable «x» es 2).

Jugando con los componentes

Adelgazándola o enanchándola.

Si queremos que «adelgace» y se vea más estrecha, tenemos que multiplicarla por un número mayor que la unidad (por ejemplo: 5x2)…

Y si queremos que «engorde» y se vea más ancha, multiplicamos por un número menor que la unidad (por ejemplo: 1/3 x2)…

Así, cuanto mayor sea el coeficiente por el que multiplicamos más estrecha se ve la parábola, y cuanto menor sea dicho coeficiente más ancha se ve…

Antes de seguir, es muy importante dejar clara una cosa. Las parábolas son todas semejantes, y como tales tienen la misma forma en realidad.

Lo que ocurre es que el cambio de escala nos hace ver que la parábola se «ensancha» o se «estrecha», pareciendo que cambie su forma.

Vamos ahora a desplazarla verticalmente.

Esta parte es bastante intuitiva, ya que simplemente tenemos que sumar o restar las unidades que queremos que suba o baje respectivamente la parábola.

Así, por ejemplo, si queremos moverla hacia arriba tres unidades le sumamos 3…

Y si queremos bajarla dos unidades le restamos 2…

Se vería así, una posible secuencia:

Desplacémosla ahora horizontalmente

Para moverla hacia la izquierda, tenemos que sumarle a la «x» que está elevada al cuadrado las unidades que queremos desplazarla, y para moverla hacia la derecha tenemos que restárselas.

Por ejemplo, para desplazarla a la izquierda dos unidades le sumamos a la «x» que está al cuadrado un 2…

Y para moverla a la derecha, por ejemplo, cuatro unidades le restamos a la «x» que está al cuadrado un 4…

Otra pequeña animación:

… ¿qué nos falta?

¡Ponerla «boca abajo»!

Digamos que lo que queremos hacer es cambiar la concavidad de la parábola, pasando de ser cóncava hacia arriba (convexa) a cóncava hacia abajo (cóncava), y el vértice de la misma pasa también de ser el mínimo de la función a ser el máximo.

Conseguirlo es bastante sencillo, ya que tan solo tenemos que poner un «-» delante del término que está elevado al cuadrado.

Por ejemplo…

 

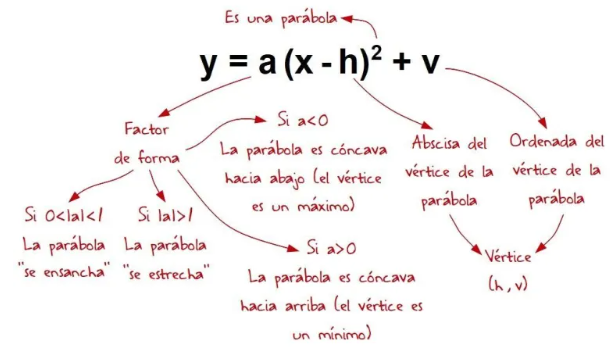
Como ayuda memoria…

Y todo esto que hemos visto por separado para que se entendiese mejor, se puede dar, como es lógico, simultáneamente.

Por ejemplo, si tenemos la función:

Podemos deducir directamente que…

Todas estas conclusiones sin realizar ni un sólo cálculo.

Y ésta sería su representación gráfica:

Pues esta forma de escribir la función cuadrática es la que se conoce como forma canónica.